近日,我校数学科学学院卢琳璋教授团队在人工智能领域1区TOP期刊Expert Systems With Applications(IF=7.5)上发表了题为“Multi-graph regularized non-negative tucker decomposition and its semi-supervised extension for image clustering”的研究论文。

非负Tucker分解(NTD)是一种提取张量数据低维表示的常用技术,但其本质是无监督的。图作为呈现数据空间几何信息的重要方式,已被广泛使用。许多基于图的NTD方法已被提出。然而,这些方法在利用图时依赖于数据空间的单一表示,而忽略了数据空间的其他有意义的表示形式中的图。为了解决这一局限性,我们构造一个多图正则化并引入到 NTD中,提出一种多图正则化NTD(MGNTD)方法。该方法能提取一个有效的保留了原始数据空间中的多种图结构的低维表示。此外,我们融入少量标签信息到该方法中,将它扩展为一种半监督方法—多图正则化半监督NTD(MGSNTD)。该方法能通过传播标签信息并保留数据空间中的多图结构,提取到一个更好的低维表示。针对这两种方法,文中给出了有效的求解算法,并分析了相应的收敛性。在真实数据集上的大量实验结果表明这两种方法的有效性。
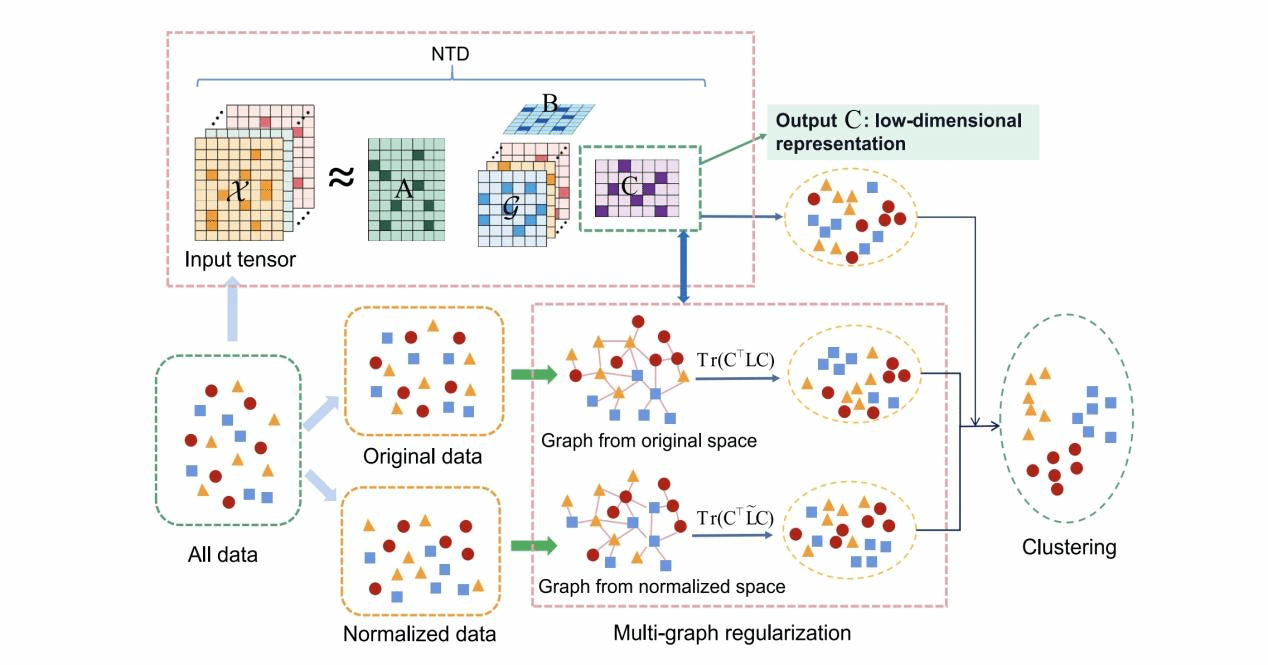
MGNTD总体框架
MGNTD具体模型如下:
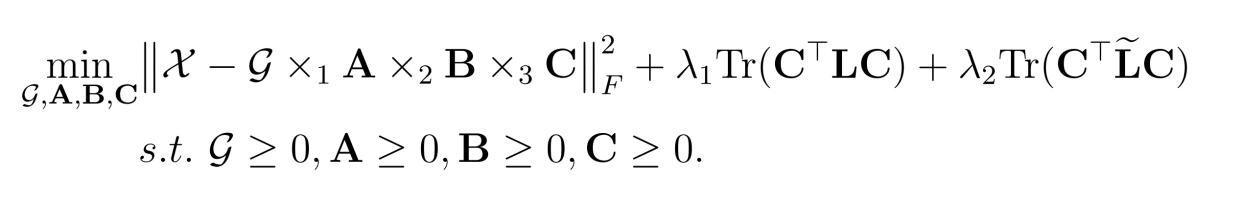
MGSNTD的具体模型如下:
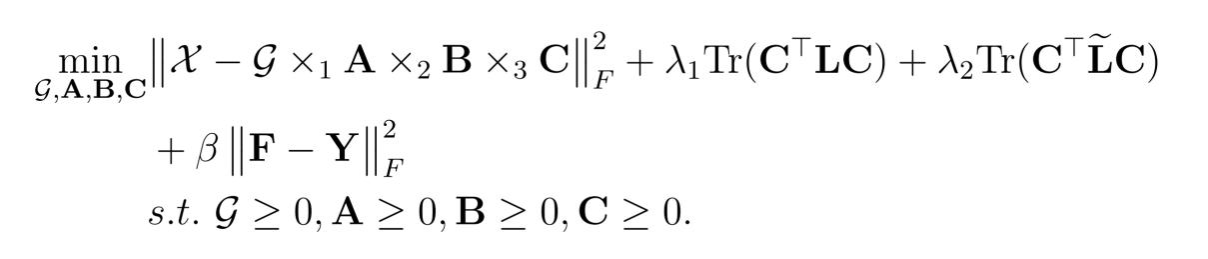
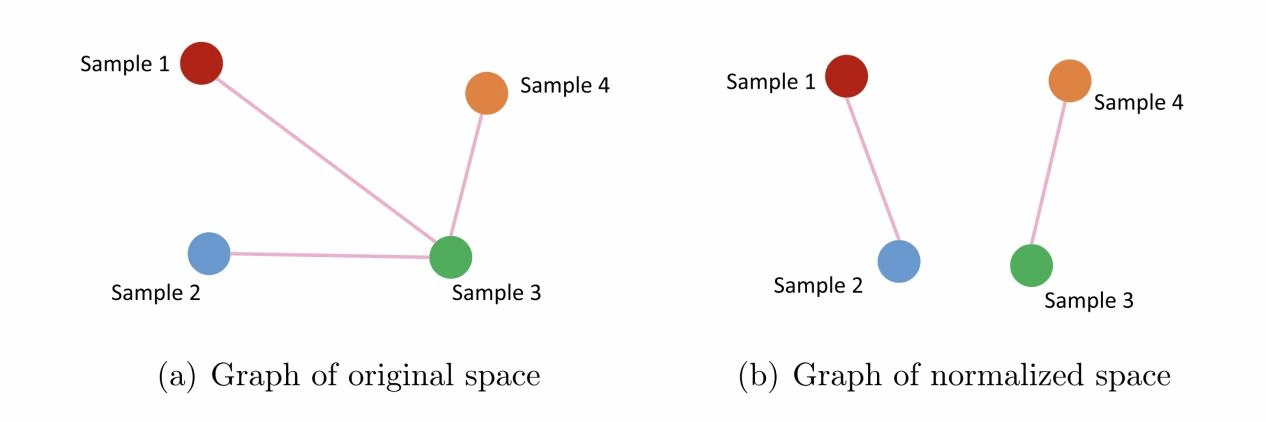
相同数据空间的不同表示形式中的图结构
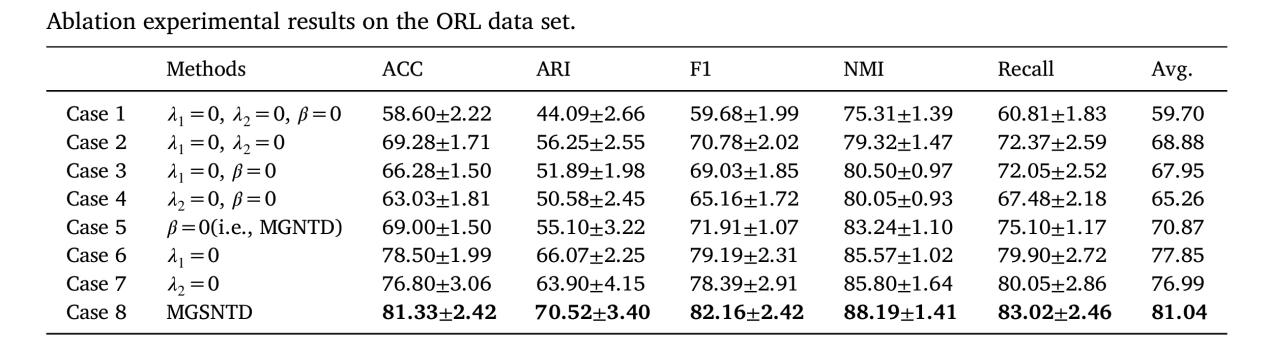
MGNTD与MGSNTD在ORL数据集上的消融实验结果
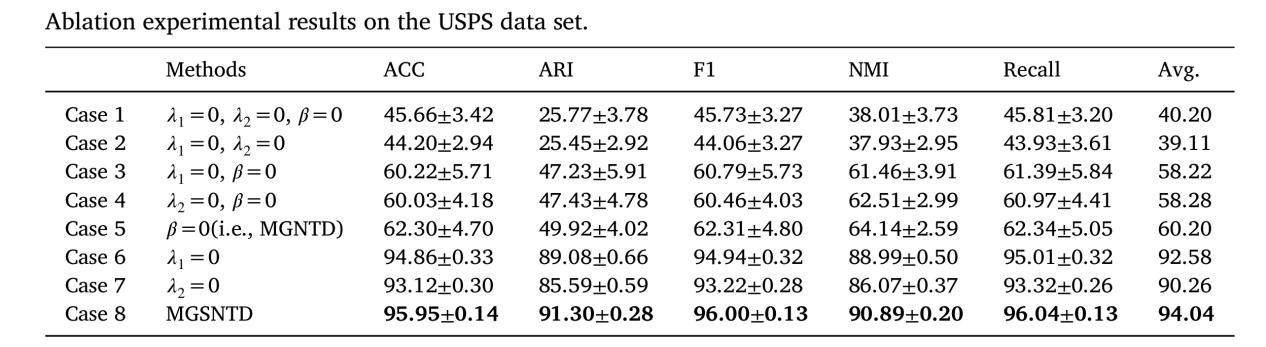
MGNTD与MGSNTD在USPS数据集上的消融实验结果
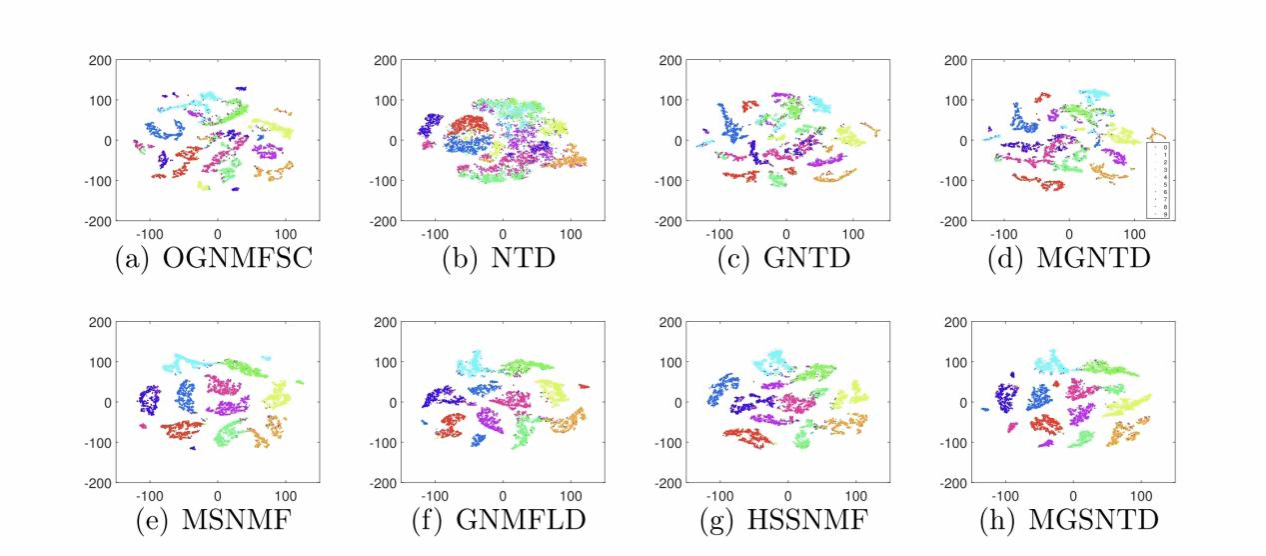
提出方法与SOTA方法所提取的低维表示的t-SNE可视化结果
该研究在常用的真实数据集上进行了大量的聚类实验。实验结果表明,提出的无监督MGNTD方法与其它无监督方法比较,在大部分情况下取得了最好的结果;半监督MGSNTD方法与其它半监督方法相比,取得了最好的性能。特别地,在不同数据集上的消融实验进一步表明了文中引入的多图正则化的有效性,即考虑数据空间的多个有意义的表示形式中的图结构优于仅考虑数据空间的单个表示形式中的图结构。这一处理和分析图的方式区别于通常的分析图的方式,它在分析数据空间的图结构方面呈现了一种不同的视角。
该论文是由数学科学学院卢琳璋教授指导的博士生景文静、卢琳璋教授、刘奇龙副教授、陈震教授共同完成。该研究得到国家自然科学基金项目(12161020,12061025,12461072)的资助。
一审:熊胜兰
二审:唐树安
三审:吴云顺

